轻云pdf压缩编辑官网
本文共 341 字,大约阅读时间需要 1 分钟。
PDF文件作为日常办公中常用的文档格式之一,文档中可包含表格、图片、文字等内容,所以PDF文件体积通常会比较大。但是有时体积太大是个问题,这时候我们就需要压缩,那么用什么方法压缩pdf最好呢?今天小编就给大家介绍一个压缩pdf又好又快的方法:
第一步:点击打开轻云pdf编辑压缩官网: www.qingyunpdf.com 打开轻云pdf编辑压缩官网,上传pdf文件,上传完毕后网站会自动压缩。
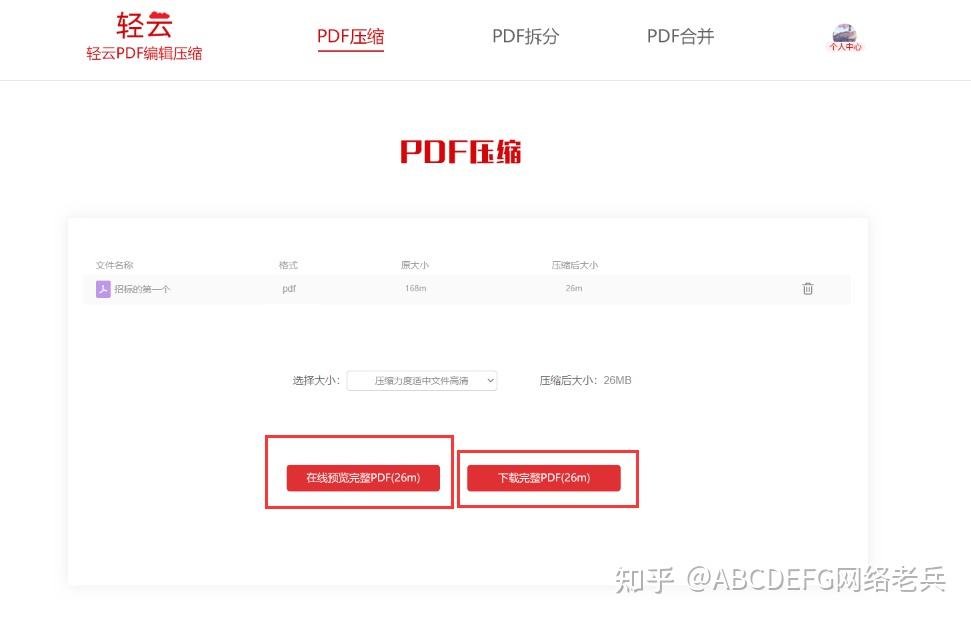
转载地址:http://yyav.baihongyu.com/
你可能感兴趣的文章
mysql 数据库存储引擎怎么选择?快来看看性能测试吧
查看>>
MySQL 数据库操作指南:学习如何使用 Python 进行增删改查操作
查看>>
MySQL 数据库的高可用性分析
查看>>
Mysql 数据库重置ID排序
查看>>
Mysql 数据类型一日期
查看>>
MySQL 数据类型和属性
查看>>
Mysql 整形列的字节与存储范围
查看>>
MySQL 是如何加锁的?
查看>>
mysql 更新子表_mysql 在update中实现子查询的方式
查看>>
MySQL 有什么优点?
查看>>
mysql 权限整理记录
查看>>
mysql 权限登录问题:ERROR 1045 (28000): Access denied for user ‘root‘@‘localhost‘ (using password: YES)
查看>>
mysql 查看锁_阿里/美团/字节面试官必问的Mysql锁机制,你真的明白吗
查看>>
MySql 查询以逗号分隔的字符串的方法(正则)
查看>>
MySQL 查询优化:提速查询效率的13大秘籍(避免使用SELECT 、分页查询的优化、合理使用连接、子查询的优化)(上)
查看>>
mysql 死锁 Deadlock found when trying to get lock; try restarting transaction
查看>>
mysql 死锁(先delete 后insert)日志分析
查看>>
MySQL 死锁了,怎么办?
查看>>
MySQL 深度分页性能急剧下降,该如何优化?
查看>>
MySQL 深度分页性能急剧下降,该如何优化?
查看>>